I ran this back on 2010 as part of my W&T series. I’m including it here for completeness.
God came from Teman… He stood, and measured the earth. (Habakkuk 3:4,6)
Who hath measured the waters in the hollow of his hand, and meted out heaven with the span, and comprehended the dust of the earth in a measure, and weighed the mountains in scales, and the hills in a balance? (Isaiah 40:12)
In my first post over at Wheat and Tares (check it out if you missed it), I mentioned one of my favorite books, Mathematics for the Million. I also took an example from it on how to calculate the value of PI using reason.
This book also gives several interesting examples of other things that you can do with math. Did you know that you can mathematically calculate the size of the earth, the distance to the moon, and the size of the moon? Did you know that if you know the trick, you can form a right angle without a tool?
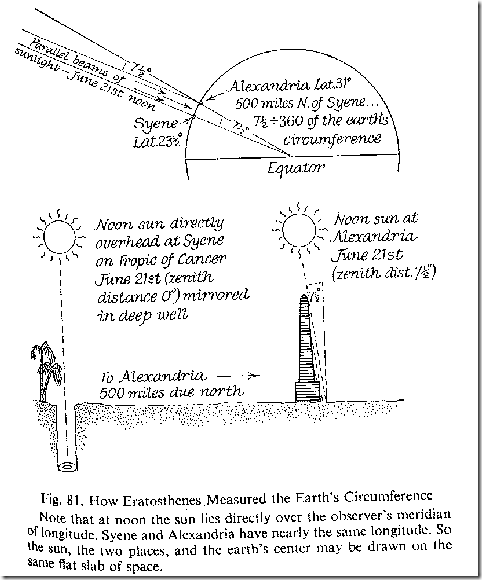
Measuring the Earth’s Radius and Circumference
The trick to measuring the Earth’s circumference is to find a well that the sun directly passes over so that you can see the reflection at the bottom of the well. This can only happen on the tropic of cancer, and only on June 21. At the same time that happens, also measure the angle of the shadow at some distance away but at the same longitude. The book uses the example of Syene and Alexandria.
Now all you have to do is use Trig to figure out the angles and sizes of the triangle that forms between the earth’s center and the two cities. It’s a bit of work, but it’s obvious that it will work. [1]
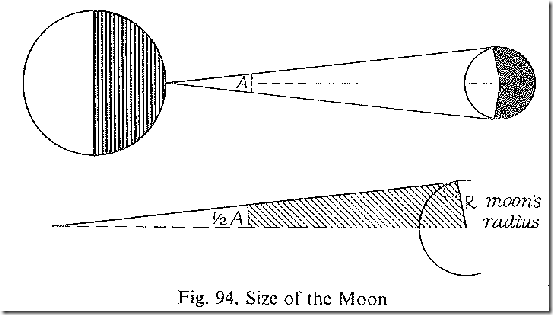
Measuring the Moon
It’s even easier to measure the moon. Now that we know the radius of the earth, we can take measurements on a single longitude of the angle of the moon. Now we use Trigonometry to calculate the distance to the moon.
By measuring the angle of the top and bottom of the moon, we can now measure the size of the moon itself.
Ancient Right Angles
This one is my favorite. Suppose you wanted to measure out a right angle, but didn’t have a compass or square because they hadn’t been invented yet. Could you do it using only high school mathematics? You can, actually, you probably just haven’t thought it through all the way.
Do you remember learning in high school that all right triangles (i.e. a triangle with one of its angle at a right angle) will follow the Pythagorean theorem?
(A^2)+(B^2)=(C^2)
One of the easiest solutions for the Pythagorean theorem (and one of the most common right triangle ratios on the GRE) is the 3:4:5 ratio. Try it:
(3^2) + (4^2) = (5^2)
9+15 = 25
So if you need a right angle, just take any measure you want and mark out on a rope 3 units, four units, and five units. Now stake the marked points down. Viola! Instant right angle. No wonder Pythagoras founded a secret cult and tried to hide his mathematical knowledge from the world.
Again, we see how mathematics is just simple logical steps that build up into something complex and beautiful. Yet when we are done, we know its right. There just isn’t any question.
It’s also interesting that these are all areas that, as the Bible quotes above indicate, were once the sole domain of God.
Notes
Images are from Mathematics for the Million, pages 207, 228, 229 respectively.
[1] See Mathematics for the Million p. 207 for details.



Pingback: Tweets that mention » Measuring the Earth and Moon The Millennial Star -- Topsy.com
I suppose I should not have immediately blocked out all trigonometry the moment I left college. It would probably have helped me in a variety of ways, not least of which helping my teenage kids with their homework and reading this post.
Fun. I wish I knew more math.
This can only happen on the tropic of cancer, and only on June 21.
I am pretty sure this can happen anywhere between the Tropic of Cancer and the Tropic of Capricorn, and in most of those places on two days out of every year.
Oh, yes! And on the Tropic of Capricorn — that’d be on December 21st, I’d suppose.
Mark,
Thanks for the correction. I’m thinking I misread that part of the book.
Bruce, here is an item I wrote a few years ago that you would enjoy: “Pondering: The Reals from the Rationals.”
Geoff and Brian, the site is getting slow again.
Jack/Bruce, Mark D is correct. It is not merely *on* the Tropic of Cancer or Tropic of Capricorn, it is on _any_ lattitude that is _between_ (and including), the Tropic of Cancer and Tropic of Capricorn, that this measurement may be performed, that the sun will be directly overhead twice a year at any given spot.
(But at the Tropic of C/C, it technically happens once a year at each, since it is at a “tangent” (sort of) point, and not a place where the transit happens twice yearly.)
The day of the year in which this happens depends on the lattitude. When it happens on the Equator it is called an “Equinox”, and when it happens at the Tropic of Cancer or Capricorn it is called a “Solstice”.
There are 2 “Equinoxes” and 2 “Solstices”. Think of a sine wave (sort of, maybe not exactly) where one cycle starts at the equator, goes up north to the Tropic of Cancer, back to the Equator, down south to the Tropic of Capricorn, and back to the Equator.
On dates between Equinoxes and Solstices, the “sun directly overhead at local noon” is happening _somewhere_ (at some lattitude) every day between those two maximum lattitudes, ie, somewhere in the “Tropical Zone”.
The “Tropic of Capricorn” and the “Tropic of Cancer” are single “circles of lattitude” parallel to the Equator, 23° 26′ 16″ south,
23° 26′ 16″ north, respectively.
Bookslinger. Awesome!
You write, “[W]e see how mathematics is just simple logical steps that build up into something complex and beautiful. Yet when we are done, we know its right. There just isn’t any question.”
This reminds me of something I said once:
“What philosophers do is make logical demonstrations. A logical demonstration is not an ‘imaginative or creative theory’. It can be shown wrong only when its logic is shown to be invalid, or when its premises are shown to be false. If the premises are accepted as true, and if the reasoning is not shown to be invalid, then it cannot be supplanted by a ‘superior theory’.”
And I pointed out to you that the disagreement was always over the premises. And I also pointed out that you could improve a theory’s fit to reality (thus making it in a sense superior) via improved premises (such as Euclidean Geometry to Euclidean geometry).
But, alas, the the conversation ended there with you continuing to object to things I didn’t say and wasn’t disagreeing with you over. *sigh*